深入探究類神經網路！——類神經元的運算
類神經元模型
符號函數 類神經元模型
類神經元模型
在本章節中，我們再次呈現Warren McCulloch和Walter Pitts的類神經元模型，
這時候，你應該更加理解𝜃值的用意，以及符號函數的功能，
試著操作下方的介面，讓自己更加熟悉這個概念吧。
(
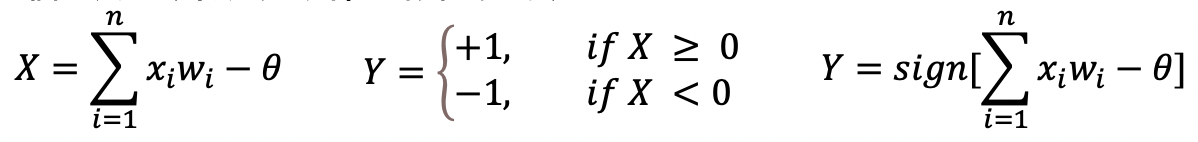
試著在方格中輸入數字，並按下計算)
0
(試著在方格中輸入數字，並按下計算)
0
思考一下，回答問題
問題一
假設X = 3·x1 + (-4)·x2 - 2，
並且Y = sign(X)，
當x1 = -2、x2 = 3 時，
請問Y值為多少？
問題二
假設X = (-0.5)·x1 + 7·x2 + 2·x3 + 6，
並且Y = sign(X)，資料以(x1, x2, x3)表示，
請問(3, 1, 2)和(-1, 2, -1)這兩筆資料，
是否分為同一個類別？
重點總結
在本章節中，我們用圖像的方式再次深入認識類神經網路，
在問答的過程中，相信你也體會到資料能夠在類神經網路處理過後被分類成某個類別，
但我們還沒介紹到，我們到底如何讓類神經網路「學習」到這樣的分類方式，
我們不只希望做出一套分類方式，還希望找到一個能夠精確分類的方式，
沒辦法百分百正確的話，至少也不要頻繁地出差錯。
在下個章節中，我們將多補充一些激勵函數的概念，
在最後一個章節，我們就能夠介紹到類神經網路如何「學習」了，繼續加油吧。
回到最上方