電腦學會如何學習了嗎？——類神經網路學習分類

類神經網路如何自動調整權重？

誤差與學習演算法 學習分類昆蟲資料 激勵函數與學習演算法

誤差與學習演算法

學習演算法是透過誤差進行權重的調整，

我們在理解學習演算法之前，先回顧一下誤差的概念吧。

(試著在方格中輸入數字，並按下計算)

在1958年時，Frank Rosenblatt提出的學習演算法：

w_i^t+1 = w_i^t + 𝛼 * x_i * Error^t

(演算法中的「error」即為「誤差」)

雖然我們說明了這個演算法為何這樣設計，

但為了更容易理解這個演算法設計的用意，

讓我們用先前健康照護的例子來理解這個演算法吧。

(試著在方格中輸入數字，並按下計算)

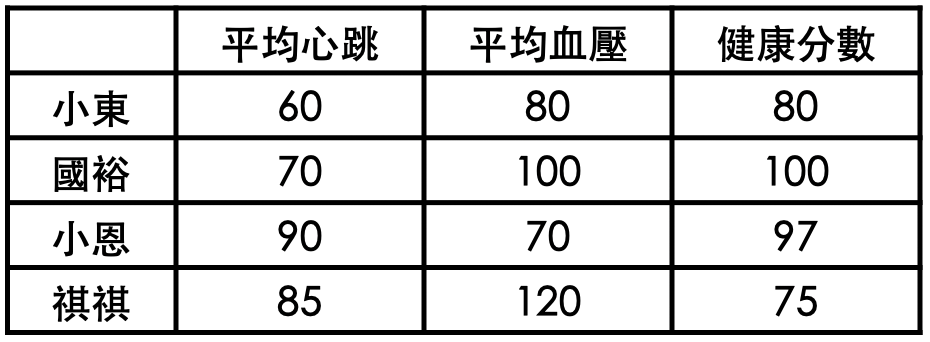
我們以小恩的健康資料來看，

起初類神經網路的權重皆為0的時候，

誤差即為97分，此時調整權重的算法會如下圖：

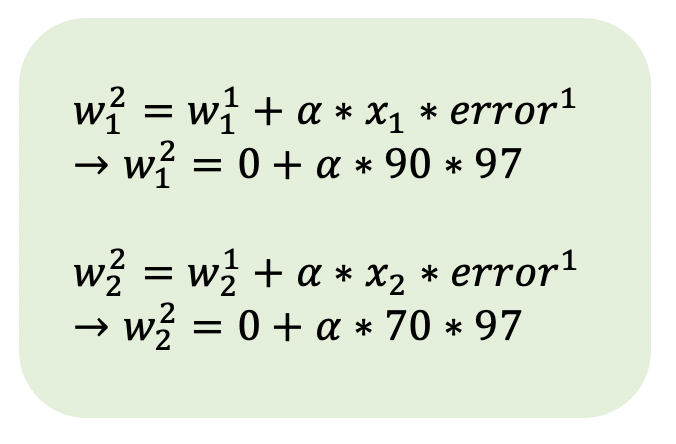
此時，我們可以看到𝛼值，也就是「學習率」是沒有設定好的，

不過這樣也更能看出「學習率」的用意，

如果𝛼值設定為1，則權重就會被調整太多，

依照資料當中的數值，我們應該將𝛼值設定小一些。

假如我們將𝛼值設定為0.0001則權重的調整就會如下：

此時，類神經網路計算第二次迭代的健康分數(y值)：

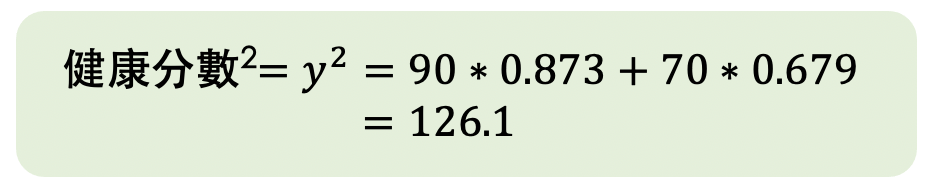
以及第二次迭代的誤差：

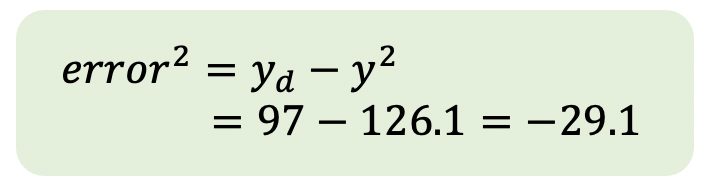
接著再計算第三次迭代的權重：

而第三次迭代的健康分數(y值)：

而在上述的運算過程當中，

值得注意的是「誤差」的大小以及正負對於權重調整的影響，

起初類神經網路的誤差較大(97分)，在第二次迭代誤差較小(-29.1分)，

所以在計算第二次迭代的權重時，調整幅度較大。

而因為正負的不同，也讓計算第二次迭代的權重時，是往正方向調整；

計算第三次迭代的權重時，則是往負方向調整。

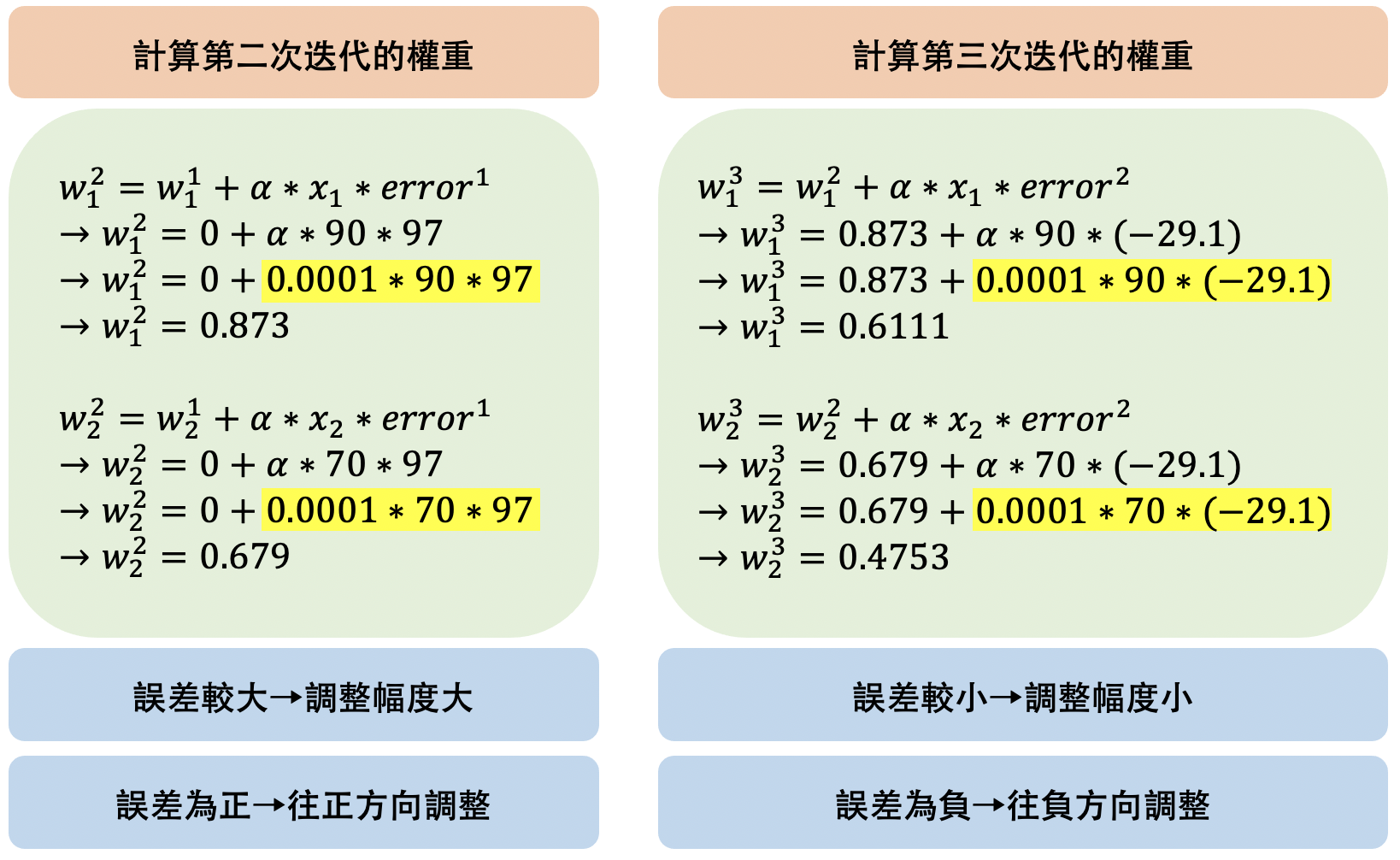
我們以動畫回顧上述的過程：

不過，在此例需要注意一個小細節，

權重調整的方向，是同時受到輸入值(x_i)以及誤差(error^t)影響，

若將上述算式的輸入值改為負值，權重的調整方向則會相反。

(試著勾選選單，並觀察權重調整的情況)

權重調整後，也會改變類神經網路的輸出值，

而每次的調整都可能讓誤差降低，

誤差越小，權重調整的幅度就越小，

這也影響著類神經網路每次逼近期望輸出的幅度，

隨著類神經網路的輸出值越靠近期望輸出，類神經網路下一次逼近的幅度就會越小。

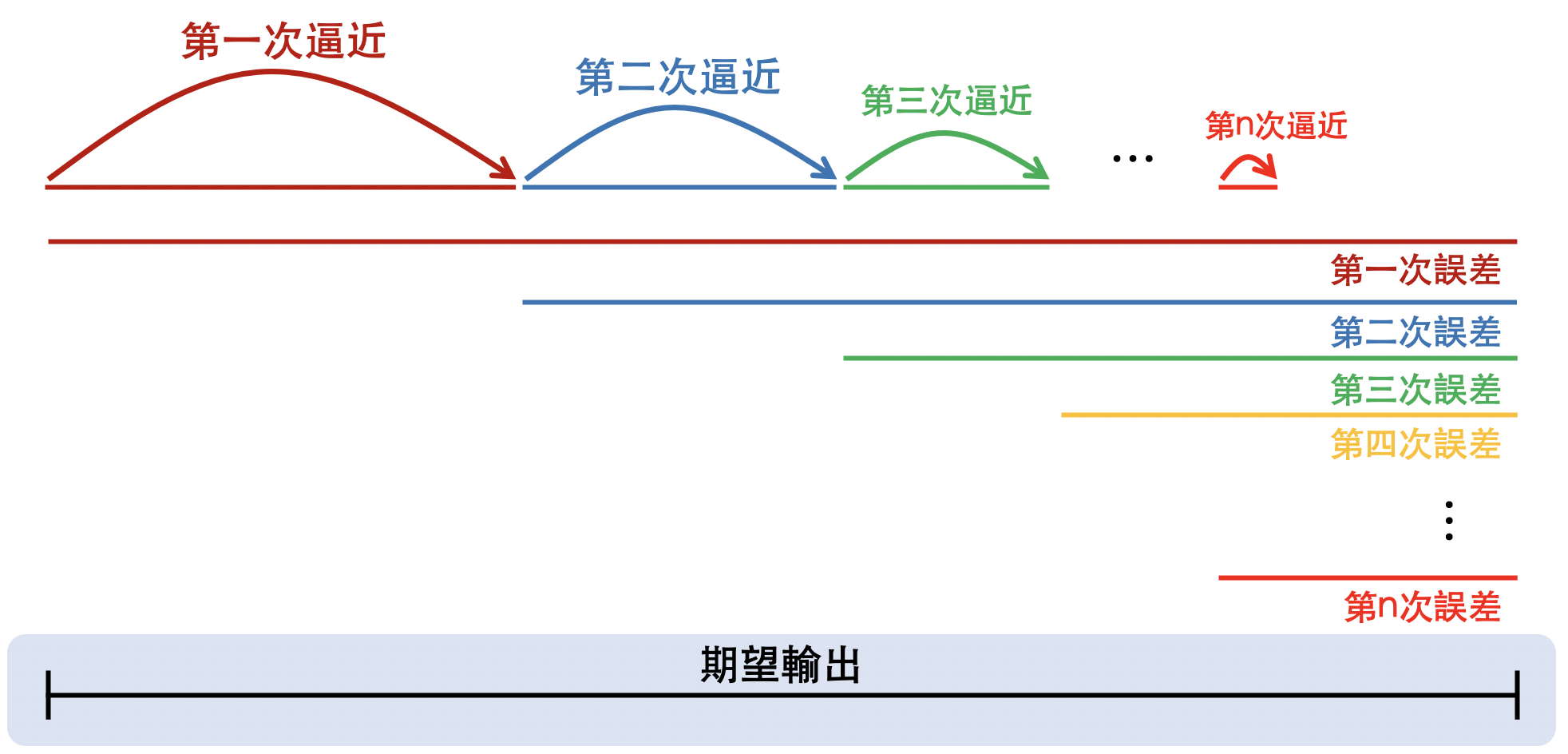
我們以動畫回顧上述的過程：

回到最上方